Ah, the triangle grid. Square grids are virtually ubiquitous, laying out out everything from the pixels in an epitome to houses in a urban center block. The hex grid has a decent showing as well, specially in lath games. But triangle grids – regular tilings of the 2nd airplane with equilateral triangles – just don't seem popular. I've seen claims they are useless, or that the maths is hard. But I'yard hither to prove both of these are wrong: the maths is actually easier than working with hexes, and triangles have all sorts of neat advantages.

I've worked out all the maths in my reference code on github, just it's worth explaining why and how to utilise these grids.

What is a Triangle Filigree

To be articulate, when I say triangle grid, I mean a tile map where each tile is an equal sized equilateral triangle, arranged in alternating rows (or columns).

What's important is every prison cell has exactly three neighbours. You sometimes see games with a fatigued grid of triangles, just the bodily pieces are placed on the corners. Each corner connects to six other corners, and then this is not really a triangle grid, information technology's actually a hexagon grid.

Hamla
Chinese checkers (Halma) is played on a hex grid, here styled to expect triangular.

Conversely, any game played on the corners of a hexagon grid is actually a triangle grid. Compatible hexagon grids and triangle grids are called dual because of this property.

Why Use Triangle Grids

At that place's iii main reasons why triangles are awesome:

  1. They're always planar
  2. They're simple
  3. They have nicer geometry

Planar

If you selection any three points in 3d infinite, it's possible to draw a flat aeroplane through them. So given those iii points, y'all tin can ever draw a triangle on the surface of that airplane. That's not true for polygons with more vertices. If y'all selection 4 3d vertices, connecting them to up to course a 4 vertex polygon becomes difficult to practise in a sensible unambiguous way. Polygons suffering this problem are called non-planar, and they can be a big problem in calculator graphics – nearly all realtime graphics converts everything to triangles to avoid this problem.

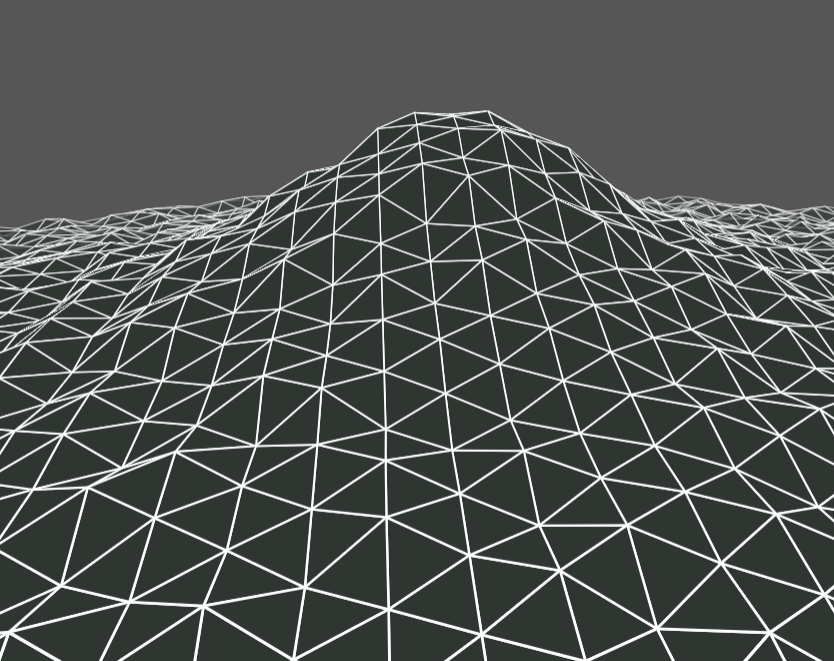
Even though I'thou here to talk about 2d tilings, this is even so a useful belongings if nosotros desire to introduce a heighmap. With a triangle grid, yous can have every vertex at a different height, and it'll notwithstanding work perfectly. Practice the aforementioned with a square grid, and yous immediately see non-planar vertices.

Sim City 2000 featured square grid and meridian maps. Note how many of the sloping tiles are split into a pair of triangles considering the tile is not-planar.
A triangle grid height map. No problems with slopes

Simplicity

It'due south a mathematical fact that 3 is less than 4 or 6 [commendation needed]. That's the smallest number of vertices a polygon tin can have, making triangles the best shape for any algorithm that scales with the number of points or edges.

For instance, when in my tutorial on Marching Cubes, I explained that you need to create \( ii^4 = 16 \) unlike tiles in order to cover all cases in 2d. That's because each of the 4 corners has ii choices. Triangles come in two varieties, upward and downwardly, and each variety needs \( 2^3 = 8 \) different tiles. So you are creating xvi tiles either way.

Note how in that location are no "cryptic" cases for triangles.

But that's but the basic case. If you let for tile rotations, then triangles accept less cases (4 vs vi). Or if you lot want more than 2 possible values at each corner (54 vs 81, or 10 vs 21 with rotations/reflections).

Rotatable tiles needed for marching cubes

Here's a ShaderToy showing marching cubes on a triangle.

Triangles are also good for linear interpolation. Interpolating three values accross a triangle is straightforward with Barycentric Co-ordinates, while squares require bilinear interpolation which is fundamentally more complex. This departure is why Simplex Noise was invented to replace Perlin Noise – they work the aforementioned, but simplex noise uses a triangle grid (in second).

Amend Geometry Than Hexes

When working with hexes, you quickly realize their edges are a huge pain. They don't line in a direct line! That makes it incommunicable to subdivide the grid with a line. You cannot build a big hex out of lots of little ones.

In the adjacent section, we'll rely heavily on straight border lines for intuition about how triangle grids piece of work.

Triangles are also very good if you lot are working on a sphere (east.thou. for a planet simulator) – information technology'southward possibly to brand a uniform sphere mesh out of simply triangles, but using squares or hexes requires having some special areas that behave oddly, like the poles, or the pentagons on a traditional football blueprint.

Absolutely, triangle grids do take their own geometry annoyances, mostly to do with how you lot need to handle triangles pointing in different directions.

How to Employ Triangles Grids

Brevity Alert: This tutorial covers concepts and ideas more than methods and lawmaking. If yous are more interested in the implementation, make sure you cheque out the reference implementation I've made.

Ok, I should preface this section by maxim there are many different ways to work with triangle grids. What I'm going to describe hither is the 1 I think is best – information technology's simple to understand, and has uncomplicated expressions for virtually everything y'all are probable to practise with triangles. I'm going to describe triangle bundled in rows ("upward-down" triangles), but everything works similarly for grids rotated 90 degrees.

The trick is to think of a triangle grid equally divers by three sets of evenly spaced parallel lines overlaid on each other:

The space between each of those parallel lines are called lanes. We'll call the three dissimilar directions of lanes a, b, and c, and number the lanes in gild.

Then the co-ordinate for a triangle is simply iii integers a, b, c which depict what lanes the triangle tin can exist plant in. It's that unproblematic!

You might be wondering why we use 3 numbers to represent a cell in a 2d filigree. Information technology just works out more conveniently this way. If you try use a two-number according system, you cease up having to make more fifty-fifty-odd exceptions or other inconsistencies. A similar fox is used when working with Hex grids, see this article on "cube" co-ordinates for hex grids. The third according is mostly redundant though – in this organisation a + b + c e'er sums up to either one or 2. And so you could but store a, b and an extra boolean.

Note there's no triangle with co-ordinates (0, 0, 0). I've numbered the lanes so that the origin is really a vertex, surrounded by the 6 triangles in lanes 0 and 1. The system works but too with different lane numberings.

Neighbours

Whenever yous move from one triangle to another, you are crossing i of the lines separating lanes. I've arranged it so that to move out of a downwards pointing triangle, you add together i to a co-ordinate. And for an up triangle, you decrease one.

                def tri_neighbours(a, b, c):     """Returns the tris that share an edge with the given tri"""     points_up = a + b + c == two     if points_up:         return [             (a - 1, b    , c    ),             (a    , b - i, c    ),             (a    , b    , c - 1),         ]     else:         return [             (a + ane, b    , c    ),             (a    , b + 1, c    ),             (a    , b    , c + 1),         ]

Triangle Center

Because moving to next triangles is e'er a step of a given size in one of the three lanes, the given triangle can be found only by summing upward all the steps taken in the three different directions.

                def tri_center(a, b, c):     """Returns the center of a given triangle in cartesian co-ordinates"""     return ((       0.5 * a +                      -0.five * c) * edge_length,             (-sqrt3 / 6 * a + sqrt3 / 3 * b - sqrt3 / vi * c) * edge_length)

Triangle Distance

As every stride is irresolute a according by one, the formula for distance is just the deviation in each according.

                def tri_dist(a1, b1, c1, a2, b2, c2):     """Returns how many steps one tri is from another"""     return abs(a1 - a2) + abs(b1 - b2) + abs(c1 - c2)

I hash out an alternative distance part in a followup article.

What triangle is a point in

To locate the triangle containing a given bespeak, you just need work out what iii lanes the triangle is in. This can exist done by measuring the distance perpendicular to the lane from the origin, hands washed with a dot product, then truncating from a floating point to an integer.

                def pick_tri(ten, y):     """Returns the triangle that contains a given cartesian co-ordinate point"""     return (         ceil(( 1 * x - sqrt3 / three * y) / edge_length),         floor((    sqrt3 * two / 3 * y) / edge_length) + 1,         ceil((-1 * 10 - sqrt3 / 3 * y) / edge_length),     )

ceil rounds a number up to the nearest integer, and floor rounds downwards. You can't just round all iii lanes in the same direction or you finish upwards with difficulties when dealing with points like (0, 0), which lie at the corner of 6 unlike triangles.

Other operations

At that place's many other operations you lot might want to practise on a grid, similar measure out distances, draw lines, and rotations. All these are described in detail in my reference implementation, on github.

You can compare them to the hex grid implementation. Triangles are so much simpler than hexes that I've implemented many hexagon operations by starting time doing the equivalant triangle operation, then converting to hexes.

Hopefully I've convinced you that triangle grids are an underappreciated tool.

Triangle Grid Procedural Generation done by Tessera

Further Reading

My side by side commodity goes into some more obscure extensions for triangle grids.

RedBlobGaming'due south write upward of grids is withal the best place to get started with understanding grids. I hear they are working on an updated copy too.

I can besides recommend Justin Pombrio'southward article on pixel to hex conversions, which turned me on to how neatly this triangle system works, and how it relates to hex grids.